Souad BENYOUB

Fonctions

Objectifs
Au cycle 4, les élèves ont découvert progressivement la notion de fonction, manipulé différents modes de représentation : expression algébrique, tableau de valeurs, représentation graphique, programmes de calcul. Ils connaissent le vocabulaire de base : variable, fonction, antécédent, image et la notation f(x). Selon le mode de représentation choisi, ils déterminent une image ou des antécédents d'un nombre par une fonction. Ils ont étudié les fonctions linéaires, les fonctions affines et leur représentation graphique.
En seconde, les objectifs sont les suivants :
  • consolider la notion de fonction, comme exprimant la dépendance d'une variable par rapport à une autre ;
  • exploiter divers registres, notamment le registre algébrique et le registre graphique ;
  • étendre la panoplie des fonctions de référence ;
  • étudier les notions liées aux variations et aux extremums des fonctions.
Les fonctions définies sur un intervalle de Ensemble R permettent de modéliser des phénomènes continus. On peut confronter les élèves à des exemples de fonctions définies sur 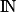Ensemble N pour modéliser des phénomènes discrets. La notation uNon est alors utilisée.
La modélisation d'une dépendance par une fonction apparaît dans des domaines très variés : géométrie dans le plan ou dans l'espace, biologie, économie, physique, sciences sociales. La modélisation de phénomènes dépendant du temps, la variable étant alors notée t est mise en évidence
Les outils numériques sont mis à profit :
  • un logiciel de géométrie dynamique, pour la représentation graphique et l'utilisation de curseurs ;
  • Python, le tableur ou la calculatrice, pour mettre en évidence l'aspect de programme de calcul.
Dans un premier temps, les élèves découvrent, manipulent et verbalisent certaines propriétés (parité, monotonie sur un intervalle…) sur les fonctions de référence. Ces propriétés se généralisent peu à peu aux fonctions quelconques. Leur maîtrise est un objectif de fin d'année. Leur formalisation est l'occasion d'un travail sur les quantificateurs.
Histoire des mathématiques
On peut évoquer la très lente élaboration de la notion de fonction, depuis l'Antiquité jusqu'à la codification actuelle par Dirichlet, en mettant en évidence quelques étapes importantes : Newton, Leibniz, Euler. On souligne alors l'importance de la notation algébrique.
Se constituer un répertoire de fonctions de référence
Les élèves doivent se constituer un répertoire d'images mentales des courbes représentatives des fonctions de référence, sur lesquelles s'appuyer lors de l'étude des propriétés des fonctions.
Contenus
  • Fonctions carré, inverse, racine carrée, cube : définitions et courbes représentatives.
Capacités attendues
  • Pour deux nombres a et b donnés et une fonction de référence f, comparer f(a) et f(b) numériquement ou graphiquement.
  • Pour les fonctions affines, carré, inverse, racine carrée et cube, résoudre graphiquement ou algébriquement une équation ou une inéquation du type f(x) = k, f(x) < k.
Démonstration
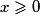  • Étudier la position relative des courbes d'équation y = x, y = x2, y = x3, pour x\geqslant 0 .
Représenter algébriquement et graphiquement les fonctions
Contenus
Fonction à valeurs réelles définie sur un intervalle ou une réunion finie d'intervalles de Ensemble R.
Courbe représentative : la courbe d'équation y = f(x) est l'ensemble des points du plan dont les coordonnées (x,y) vérifient y = f(x).
Fonction paire, impaire. Traduction géométrique.
Capacités attendues
  • Exploiter l'équation y = f(x) d'une courbe : appartenance, calcul de coordonnées.
  • Modéliser par des fonctions des situations issues des mathématiques, des autres disciplines.
  • Résoudre une équation ou une inéquation du type f(x) = k, f(x) < k, en choisissant une méthode adaptée : graphique, algébrique, logicielle.
  • Résoudre une équation, une inéquation produit ou quotient, à l'aide d'un tableau de signes.
  • Résoudre, graphiquement ou à l'aide d'un outil numérique, une équation ou inéquation du type f(x) = g(x), f(x) < g(x).
Approfondissement possible
  • Étudier la parité d'une fonction dans des cas simples.
Étudier les variations et les extremums d'une fonction
Contenus
  • Croissance, décroissance, monotonie d'une fonction définie sur un intervalle. Tableau de variations.
  • Maximum, minimum d'une fonction sur un intervalle.
  • Pour une fonction affine, interprétation du coefficient directeur comme taux d'accroissement, variations selon son signe.
  • Variations des fonctions carré, inverse, racine carrée, cube.
Capacités attendues
  • Relier représentation graphique et tableau de variations.
  • Déterminer graphiquement les extremums d'une fonction sur un intervalle.
  • Exploiter un logiciel de géométrie dynamique ou de calcul formel, la calculatrice ou Python pour décrire les variations d'une fonction donnée par une formule.
  • Relier sens de variation, signe et droite représentative d'une fonction affine.
Démonstration
  • Variations des fonctions carré, inverse, racine carrée.
Exemples d'algorithme
  • Pour une fonction dont le tableau de variations est donné, algorithmes d'approximation numérique d'un extremum (balayage, dichotomie).
  • Algorithme de calcul approché de longueur d'une portion de courbe représentative de fonction.
Approfondissement possible
  • Relier les courbes représentatives de la fonction racine carrée et de la fonction carré sur Ensemble R+.